As I pursue my PhD in physics education research, I have found time to explore a number of interesting questions. In this post, I’ll explore an approach to thinking about student reasoning in the introductory physics lab that we decided not to pursue at this time.
The Physics Measurement Questionnaire
Building on more than 20 years of development, use, and research, the Physics Measurement Questionnaire (PMQ) is a staple in introductory physics lab research. Its home is the group of Saalih Allie. This 10-question assessment is based on the following experiment:
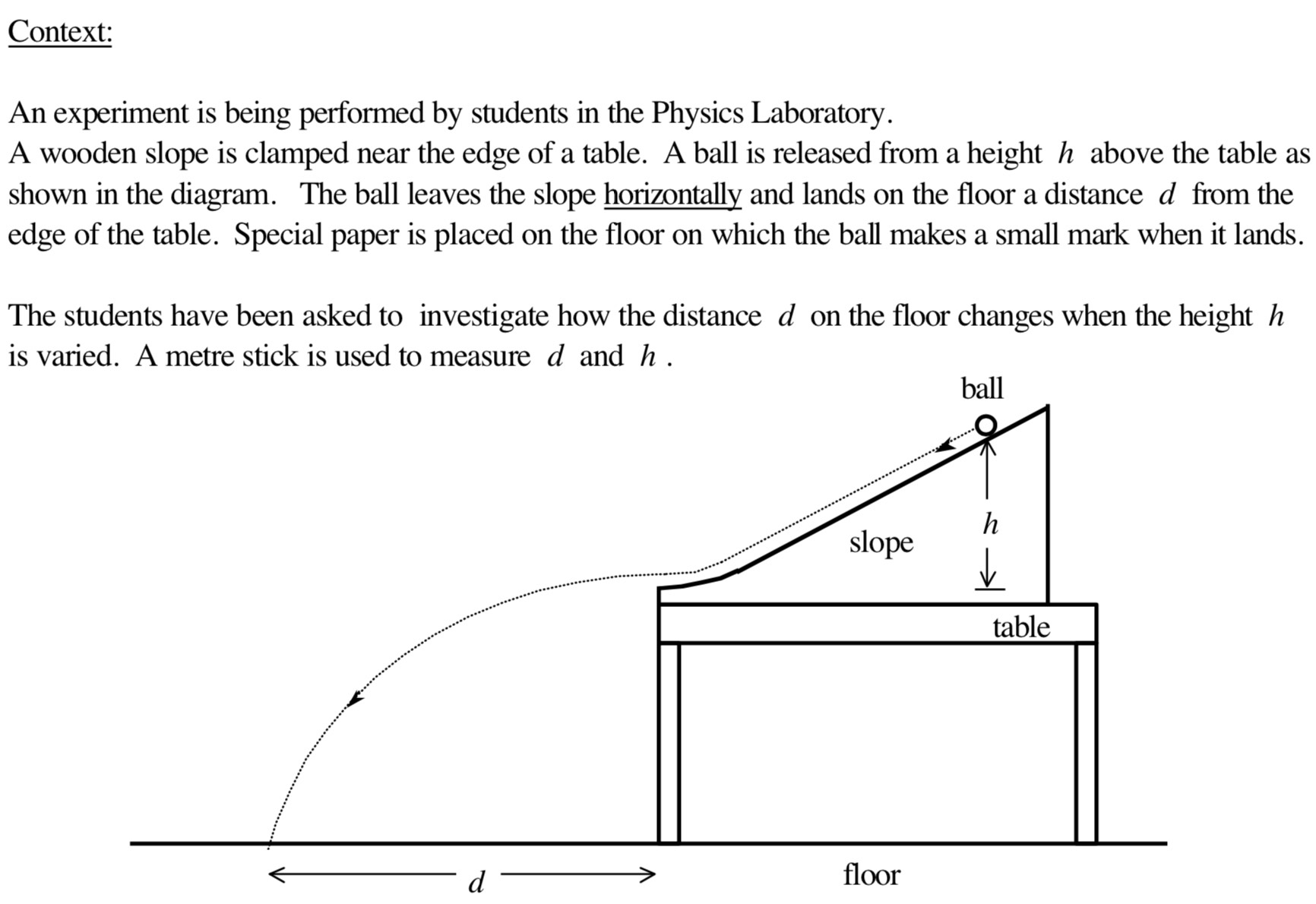
Students are asked a series of questions that seek to determine the extent to which they agree with a set of principles about how lab-work is done (at least, in the abstract). The principles don’t appear explicitly in the relevant literature, but seem to be:
- More data is better
- When collecting data, it is good to get the largest range possible for the independent variable
- The average represents a set of repeated trials
- Less spread in the data is better
- Two sets of measurements agree if the averages are similar compared with the spread in their data
These axioms feel true and, as a teacher, I see value in getting my students to understand fundamentals about the nature of scientific work. However, while they are broadly applicable, the reality of science is that none of these axioms are exactly true. There is the question of whether science has a universal “method” — Paul Feyerabend argues it doesn’t. When I sat down with a distinguished professor to look at the PMQ, the professor could identify the “right” answer, but often didn’t agree with it.
This reminds me of the “Nature of Science” that was brought into the International Baccalaureate (IB) physics curriculum in 2014. It appears in the course guide as a 6-page list of statements about how science works, culminating in this mind-bending image:
So maybe attempting to define how science works isn’t a productive approach. Fortunately, the PMQ isn’t just a test of whether students agree with certain axioms of experimental physics.
Question-Level Analysis
In addition to evaluating students on their agreement with the above axioms, the PMQ also asks students to justify their reasoning. An example question follows:

After “Explain your choice”, the PMQ includes several blank lines for the student response. The instructions suggest that students should spend “between 5 and 10 minutes to answer each question”.
A thorough analysis of student responses is possible by using the comprehensive categorization scheme in Trevor Volkwyn’s MSc thesis. Volkwyn (and the PMQ authors) view the PMQ as an assessment that aims to distinguish two types of student reasoning about experimental data collection:
Point-Like Reasoning is that in which a student makes a single measurement, and presumes that the single (“point”) measurement represents the true value of the parameter that is being measured
Set-Like Reasoning is that in which a student makes multiple measurements, and presumes that the set of these measurements represents the true value of the parameter in question
Alternatively, we could view the point-like paradigm as that in which students don’t account for measurement uncertainty or random error.
Examples of responses that conform to the point-like reasoning paradigm, for the example above, include:
- Repeating the experiment will give the same result if a very accurate measuring system is used
- Two measurements are enough, because the second one confirms the first measurement
- It is important to practice taking data to get a more accurate measurement
Examples of responses that match the set-like paradigm include:
- Taking multiple measurements is necessary to get an average value
- Multiple measurements allows you to measure the spread of the data
Thus, it is possible to conduct a pre/post analysis on a lab course to see whether students’ reasoning shifts from point-like to set-like over the course. For example, Lewandowski et al at UC Boulder have done exactly this, and see small but significant shifts.
My Data
I subjected a class of 20 students to the PMQ, and coded the responses to two of the prompts using Volkwyn’s scheme. The categorization was fairly straightforward and unambiguous.
For question 5, which asks students which of two sets of data is better (one has larger spread than the other), 17 students provided a set-like response and 3 gave the point-like response.
For question 6, which asks students whether two results agree (they have similar averages and comparatively-large spreads), only 1 student gave a correct set-like response, and the other 19 provided point-like reasoning.
I think this indicates two things:
- Different types of prompts may have very different response levels. Similar results are found in the literature, such as Lewandowski’s paper, above. This suggests that the set-like reasoning construct is complex, either with multiple steps to mastery or with multiple facets. Thus, it might not make sense to talk about it as a single entity with multiple probes, but rather as a collection of beliefs, skills and understandings.
- Some of the reasoning on question 6 seemed shallow. This suggests, for me, a bigger take-away message: my students aren’t being provoked to think critically about their data collection and analysis.
Going forward, we’ve decided not to use the PMQ as part of our introductory lab reform efforts. However, by trying it out, I was able to see clearly that our new curriculum will need to include time dedicated to getting students to think about the relevant questions (not axioms) for the experiments they conduct:
- How much data should I collect?
- What range of data should I collect?
- How will I represent the results of my data collection?
- How will I parameterize the spread in my data, and how will I reduce measurement uncertainties and random error?
- For different types of data, how can we know if two results agree?
Interestingly, some of Natasha Holmes’ work on introductory labs starts with the 5th question by asking students to develop a modified t-test, and then uses that tool to motivate cycles of reflection in the lab. That’s another approach we’ve agreed doesn’t quite work for us, but that is likewise a huge source of inspiration.